Forgetting: The challenge of teaching mathematics

Mathematics is a discipline of interconnected knowledge that is built on prior learning. Students are being asked to recall concepts, skills and procedures in order to successfully learn new material. Learning new content is next to impossible if pre-requisites have been forgotten. This makes the study of forgetting crucial.

The initial, and still relevant, scientific studies involving forgetting were conducted by Hermann Ebbinghaus in 1886. He and psychologists since his initial work have researched methods to improve recall and use the diagram at the right to show how repeated visits to the content over a period of time, helps learners remember longer.

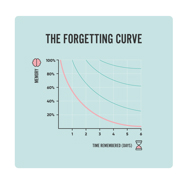It is counterproductive to teach content in large/long blocks. Teaching needs to revisit the content in a planned cycle. This type of instruction is called spaced learning and has been shown as one of the most important influencing factors for retention. (https://examstudyexpert.com/ebbinghaus-forgetting-curve/)

Spaced learning is the one overarching approach, but it does not give specific teaching strategies to be used within activities. The following ideas should be incorporated in the spaced learning approach.

Use a variety of representations – real world, concrete, pictorial, words (oral or written), and symbols
One of the greatest contributors to forgetting, is the over-use of abstract symbols. Students remember when the material is linked to real world situations, concrete objects, or pictorial images. For example, students remember the steps to divide when the process is linked to sharing.

Real context also makes it possible to use concrete materials to act out the steps. In the example at the right, money could be used to work out the answer. In the classroom, teachers will often use manipulatives to act out the steps. By using and connecting multiple representations, students are more likely to remember the process.

Three people share $465 they earned for washing cars. What does each person receive?

We will start with the hundreds. Each person will get one hundred.
                   1
               465/3

Connect new learning to what is already known
Often, new ideas in mathematics are presented in isolation. For example, multiplication facts are important and can be mastered if they are taught as a group with the same overall thinking strategies. Visual materials, like cards shown at the right, help students learn ‘x 2’ facts (2 x 3 = __, 2 x 4 = __, 2 x 5 = __, 2 x 6 __ and so on) using doubling. This helps students remember all the facts in the group of ‘x 2’ basic number facts.

Once students are confident with all of the ‘x 2’ facts, they use doubling again to learn the ‘x 4’ facts. In this way students see that the ‘x 4’ facts can be learned using the same strategic thinking.

Encourage students to be more involved in the learning
This means that students should be more active to verbalise and describe more of what they are learning. For example, they should explain what they see with these cards.

I think ‘double’ means to multiply by 2.

We can double and double again to multiply by 4.

A sample card to show one of the multiply by 2 facts.

A sample card to show one of the multiply by 4 facts.

Finally, re-visiting the content at strategic intervals means you can remember much more, for much longer. Do not be afraid to repeat discussions, with slight modifications. For example, address the same computation in a different context, with food rather than money.

In many current programs, symbols are introduced very early, perhaps because they are an efficient way of representing certain concepts. This can limit students' understanding of the concept and what these symbols represent because the symbols don’t have meaning for the students yet.  This greatly reduces their ability to make connections by applying their knowledge to new situations.

At ORIGO we introduce symbols gradually, to build a deeper understanding of the concepts underlying abstract symbols. In this way, students are better equipped with the confidence and ability to apply mathematics in new and unfamiliar situations. We encourage you to see it for yourself and give it a try with the resources we have created for at home learning. Built along a developmental scope and sequence, teachers can share these weekly plans with parents to reinforce grade level skills and standards and stop the curve of forgetting in mathematics.

Photo by leshkamal from Pexels