Teaching Algorithms in the Primary Years of the Australian Curriculum - What's New!

ACARA has introduced computational thinking as one of the mathematical processes that are embedded in the content of the new Australian Curriculum: Mathematics 9.0 (ACM).
The expression computational thinking was first used in 1980 (Papert, 1980), but was popularized by Janette Wing in 2010 (Wing, 2010). Most recently PISA, the international organisation that benchmarks student achievement around the globe, highlighted the importance of computation in their 2021 Mathematics Framework stating, “mathematical reasoning and computational thinking, provides the intellectual acumen behind problem solving in the 21st century”. As such, it can be assumed that future items in the PISA assessments will require the application of computational thinking skills. So, what is computational thinking and what does it look like in the primary classroom?
In the preamble to the ACM, ACARA describes computational thinking as a combination of five components as illustrated (by us) in the diagram below.
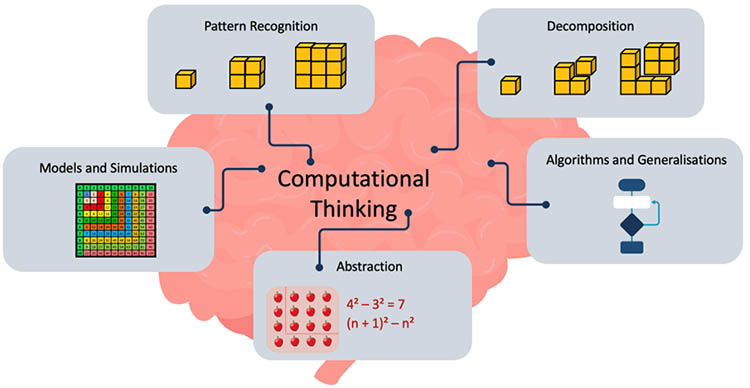
While all the above terms may be familiar to the reader, this article will explore algorithms as we believe teachers may interpret this term in a more traditional sense, rather than that intended by ACARA. In short, the ACM defines an algorithm as “a precise description of the steps and decisions needed to solve a problem or a set of rules to follow in order to accomplish a task” (ACARA, 2022). As such, traditional paper-and-pencil algorithms could fit within this definition as they provide procedures to complete the tasks of computation with whole numbers, fractions and decimals. However, as we stated in our article published here, ACARA makes no reference to traditional paper-and-pencil algorithms in the content descriptors of the primary years of the ACM. So how does ACARA want young students to work with algorithms?
The most notable change in the role of algorithms in the ACM is the requirement to have students “create” their own algorithms. And these algorithms need to be written in such a way that a computer – either human or machine – can effectively carry them out. For example, look at the elaboration that accompanies the Year 3 content descriptor below. It suggests students create an algorithm for generating multiples of 3.
| Content Description | Elaboration |
| Follow and create algorithms involving a sequence of steps and decisions to investigate numbers; describe any emerging patterns (AC9M3N07) |
Creating an algorithm as a set of instructions that a classmate can follow to generate multiples of 3 using the rule “To multiply by 3 you double the number and add on one more of the number…” |
Rather than ‘giving’ the students the rule as implied by this elaboration, it would be better if the students generate the rule from a hands-on or pictorial investigation of a pattern such as this.
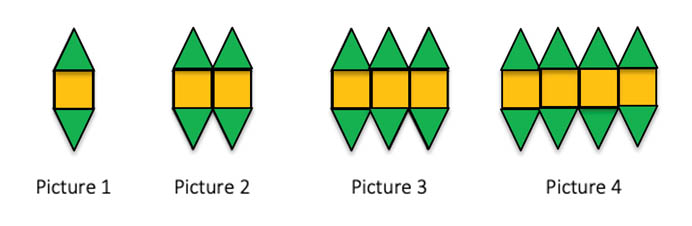
From this pattern the students can count the number of triangles and squares that are used to create each picture and record the numbers in a table such as the one below.

Try answering these questions to reveal the rule described in the elaboration.
- Look at the first and second rows. How do the numbers relate to the ‘picture numbers’ above?
- Look at the third row. How do the numbers relate to the ‘picture numbers’ above?
- Look at the bottom row. How do the numbers relate to the ‘picture numbers’ above?
The next step is to use this finding to write a rule or algorithm that can be used to create all the multiples of three. While this part could vary from student to student, a simple algorithm might read as follows:
The first multiple of 3 is calculated by doubling 1, then adding 1.
The second multiple of 3 is calculated by doubling 2, then adding 2.
The third multiple of 3 is calculated by doubling 3, then adding 3.
The fourth multiple of 3 is calculated by doubling 4, then adding 4.
And so on.
An extension from this might be to have the students generalise a rule for calculating the 10th multiple of 3 to complete the table above; then the nth multiple of 3.
Flowcharts are included in the ACM to help students follow and create algorithms. For example, look at the elaboration that accompanies the Year 4 content descriptor below.
| Content Description | Elaboration |
| Explain and use the properties of odd and even numbers (AC9M4N02) | Following an algorithm consisting of a flow chart with a series of instructions and decisions to determine whether a number is even or odd; using the algorithm to identify which elements |
In this elaboration, the students simply follow the steps on a given flowchart like this one below. Later experiences may require students to move around the individual ‘pieces’ of a flowchart to show the steps of an algorithm before they eventually create one from scratch.
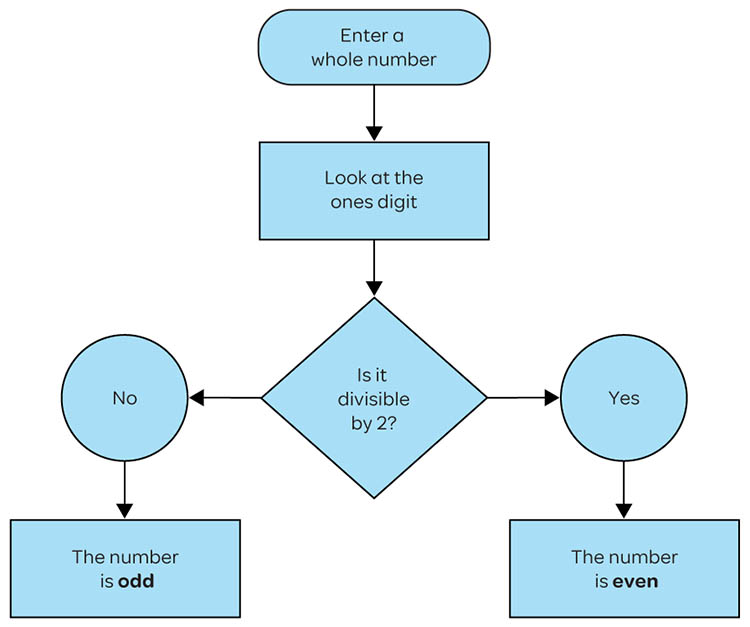
From ORIGO Mathematics Year 4
The notion of computational thinking is relatively new, but it has already been flagged as a skill that citizens and employees will need in the very near future. As such, the ACM has identified and introduced it as one of four mathematical processes that are embedded across the content from F-10. Algorithms/generalisations is one of the components of computational thinking detailed in the ACM, and unlike algorithms in past curricula, ACARA has provided sufficient detail to enable students to investigate and create algorithms that should enliven mathematics instruction. It is hoped that a side benefit in this shift of thinking will see students empowered to do mathematics in a way that makes sense to them.
References
Papert, Seymour. (1980) Mindstorms: Children, computers, and powerful ideas. Basic Books, Inc.
PISA 2021 Mathematics Framework (Second DRAFT)
JM Wing, Computational Thinking: What and Why?. Carnegie Mellon University, School of Computer Science, https://www.cs.cmu.edu/~CompThink/resources/TheLinkWing.pdf 17 November 2010.