Teaching Computation in the Primary Years of the Australian Curriculum – What’s New!

ACARA has significantly emphasised mental computation strategies in the primary years of the Australian Curriculum: Mathematics 9.0 (ACM). In fact, traditional paper-and-pencil algorithms are not mentioned in the content descriptors of any year level. This decision should be applauded and embraced as the use of written algorithms are clearly yesteryear’s skills and will not be used when today’s students enter the workforce in 2035 and beyond. This raises the questions, what computation skills should student learn and how best can these be developed?

Students need to develop a repertoire of mental strategies for addition, subtraction, multiplication, and division. A close examination of the Number and Algebra strands of the ACM reveals how this work begins with basic facts and extends to 2- and 3-digit whole numbers and beyond, and to decimals and the addition and subtraction of fractions. The ACM also includes strategies based on properties, standard and non-standard place value partitioning, using factors to multiply, compatible numbers to add, and inverse relationships to subtract and divide. Fortunately for teachers, this version of ACM provides detailed elaborations that give some insight into how these strategies can best be developed. While the purpose of this article is not to show all that detail for each strategy, it does intend to show simple models that can be used to develop key strategies for multiplication across several year levels.

It is worth noting that the ACM frequently mentions the use of hands-on or virtual materials such as arrays and area models to “develop efficient strategies” for multiplication as shown below in these Year 4 and 5 elaborations.

Array models utilise discrete objects such as the dots depicted below left. While its dimensions are 3 by 4, is has no measurable area due to the gaps between the rows and columns. Conversely, the model at the far right has a measurable area but no discrete rows and columns. In pictures such as these, values are simply assigned to the dimensions.

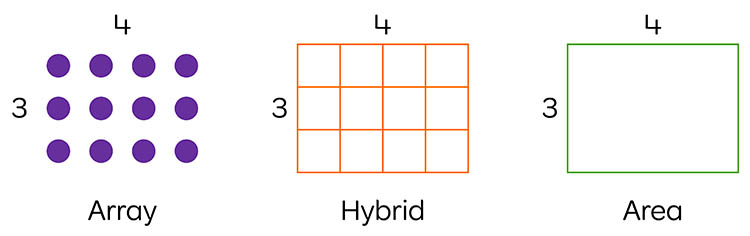
The picture in the centre above is a hybrid of the array and area models, as it has discrete countable squares and a measurable area. Hybrid models such as this are useful for showing various forms of partitioning. For example, the rectangular array below is 8 wide and 35 long. A student can use place-value partitioning to count and colour 8 by 3 tens and 8 by 5 ones. The total area is the sum of the two partial products which is now easier to calculate mentally.

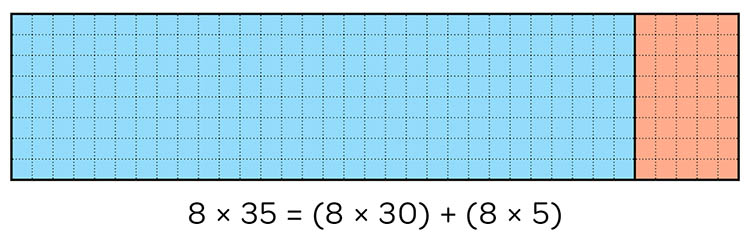
The same approach could be used to calculate the product of two 2-digit numbers. Each large array below is 12 by 35. In the first array, the student has chosen to partition 12 into tens and ones, whereas the second array shows the other dimension (35) partitioned into tens and one. While both are correct, the first partitioning is probably more helpful for calculating the total area, or product of 12 x 35.

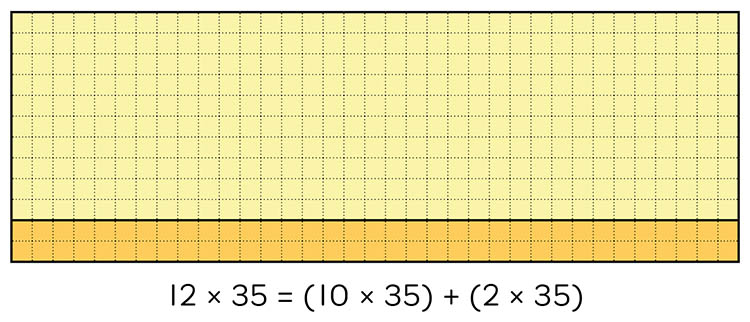
Partitioning 12 into tens and ones

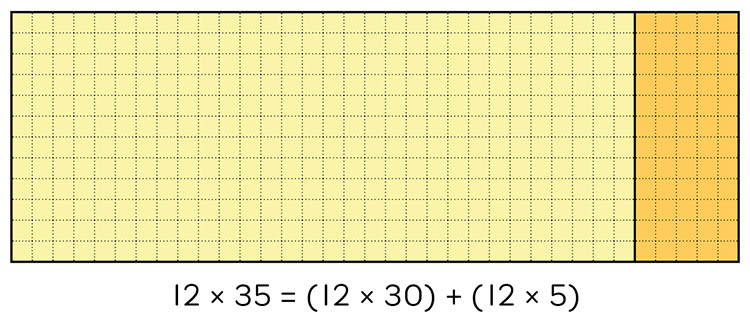
Partitioning 35 into tens and ones

If given the opportunity, some students may choose a different strategy to calculate the total area of the rectangle above. For example, they may cut the shorter dimension in half and rearrange the two smaller rectangles to make a longer rectangle as show below. In doing so, the new dimensions (factors), are much easier to multiply mentally. A student who uses this strategy understands that the total area of the original rectangle has not changed.

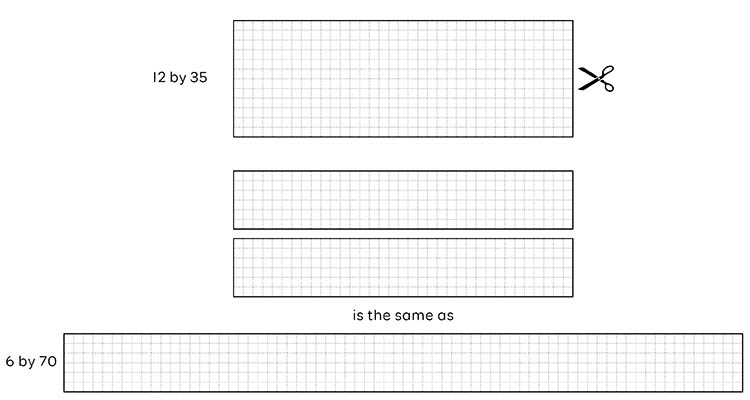
This “doubling and halving” strategy is mentioned several times in the ACM. For example, it appears in the first part of this elaboration alongside the Year 4 Content descriptor below.

The second half of that same elaboration recommends the application of the associative property. In order to use this thinking, the student would need an understanding of factors, and this is one of several reasons why there is also a renewed focus on factors and multiples in the ACM. A student may demonstrate their use of factors on the above rectangle by partitioning 12 to show 3 smaller rectangles with 4 rows in each as follows.

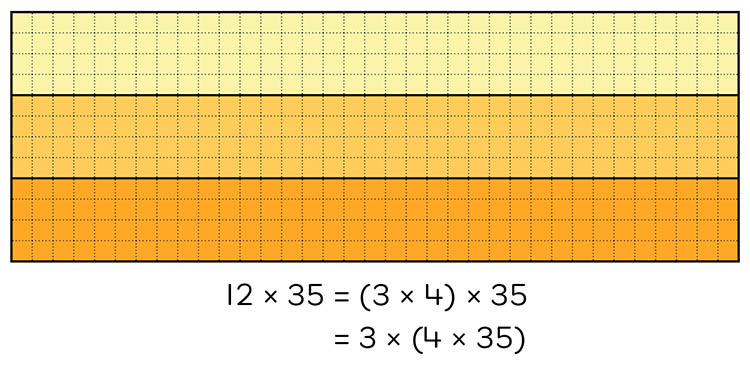
Using the factors of one number is a necessary pre-requisite for using the factors of both dimensions, as evidenced in this Year 5 elaboration below.

By using all four factors the area (product) of the same rectangle above could be calculated mentally in this way.

The array and area models are highly versatile, as they can be used to teach multiplication concepts and skills across many years. This begins in Year 2 (AC9M2N05) to show the commutative property of basic facts, and extends up the primary years to give students a picture of various mental strategies involving 2- and 3-digit whole numbers and beyond. If this foundation is well established, then the same models can be used in later years as they begin to multiply decimals, common fractions and even binomials within the algebra strand.

Furthermore, they can be used to strengthen the inverse relationship between multiplication and division. The area model below left illustrates a simple multiplication situation where the two factors (dimensions) are known, and the total area is unknown. Whereas the model on the right depicts a typical division situation where the total and one factor (dimension) is known, and the unknown is the other factor (dimension).

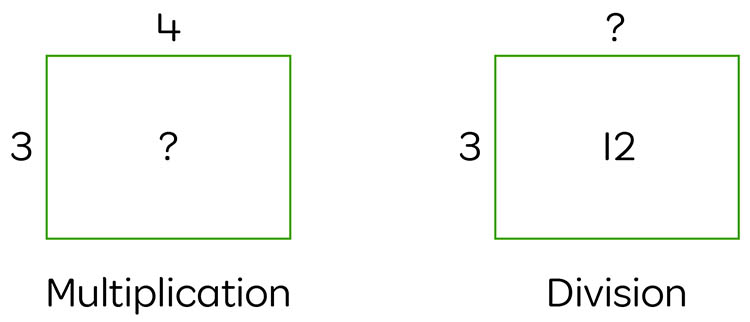
Use the link below to learn how you can register for live access and recordings of the author’s current webinar series covering this topic and so much more. https://www.origoeducation.com.au/term2_2023/