Teaching Fractions in the Primary Years of the Australian Curriculum - What's New!

ACARA has increased the focus on fractions in the primary years of the Australian Curriculum: Mathematics 9.0 (ACM). What are these changes and how might they impact your instruction?

Imagine you want to figure out how much you will pay for a $480 bicycle that has been discounted by 25%.

This is a typical problem that many people encounter in their everyday lives, which makes it a skill that all numerate individuals should master. As such, the ACM builds the foundation of percentage earlier by moving its introduction down to Year 5 as shown by the following Content Descriptor:

Recognise that 100% represents the complete whole and use percentages to describe, represent and compare relative size; connect familiar percentages to their decimal and fraction equivalents. (AC9M5N04)

While it is understood that the above problem is Year 6 content, the pre-requisites will now be developed in Year 5. This is the sequence of what you need to know in order to solve the problem.

1. 25% discount means 25% off the original price
2. To find 25% off, you need to calculate 25% of $480
3. 25% is equivalent to 25/100
4. 25/100 is equivalent to ¼
5. To figure out ¼ of 480 you need to calculate 480 ÷ 4 = 120
6. Subtract the ¼ (120) from 480 to determine the new price ($360)

Another way to calculate the new price would be to figure out 75% of the original price. In any case, the pre-requisite concepts and skills do not change. That is, much of the mental work with the percentages is actually done using common fraction equivalents. However, if you wanted to use technology to solve this problem, then you would also need a strong understanding of the relationship between percentages and decimals.

By way of the accompanying elaborations, ACM rightly suggests the use of physical and/or virtual materials to help students truly understand the concepts so they can apply them to different situations. For example, parallel number lines (mentioned in Year 4 of the ACM) are ideal for showing equivalent fraction representations.

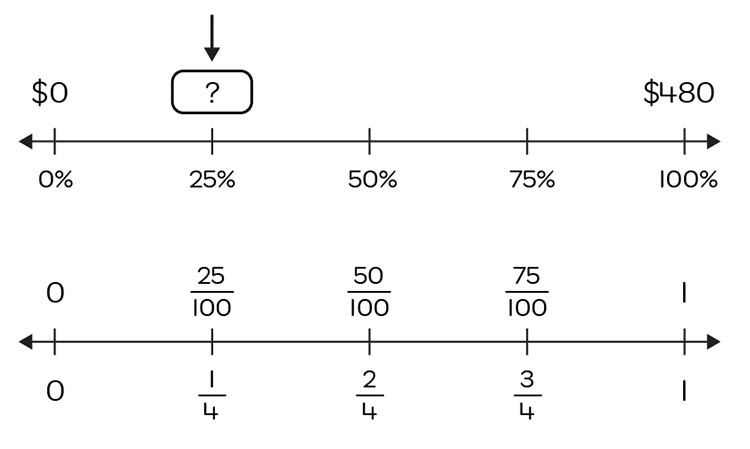
Although number lines are not ‘hands-on’ as such, they do give students a full picture of the connection among common fractions, percentages and decimals.

Area models (like this below) are another pictorial resource that can be used by students to find equivalent fractions. After colouring the first fraction, the student draws more lines to show an equivalent fraction. A key advantage of using this model is that once completed, the picture shows that the numerator (the part coloured) and denominator (the total original number of pieces) are both multiplied by the same number (3) to create an equivalent fraction. In doing so, it is building a rule for creating equivalent fractions.

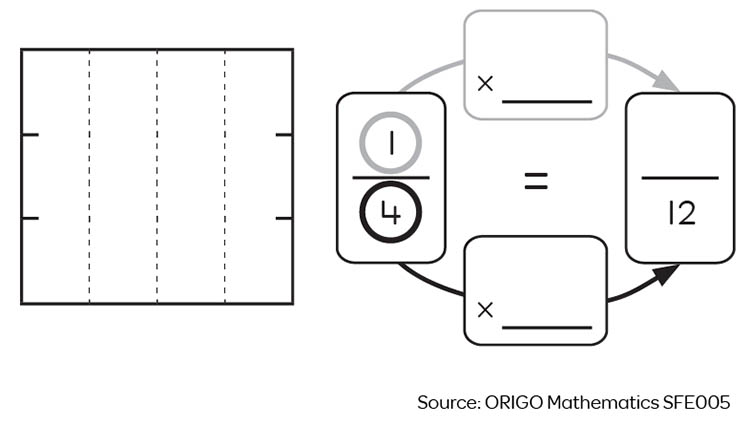
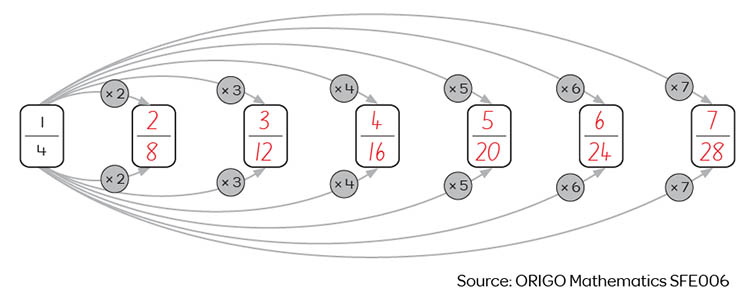
A family of common fractions equivalent to ¼.

Fraction ‘families’ can also be generated by colouring two rows of a multiplication chart as shown below. This chart shows the fraction family for 2/5.

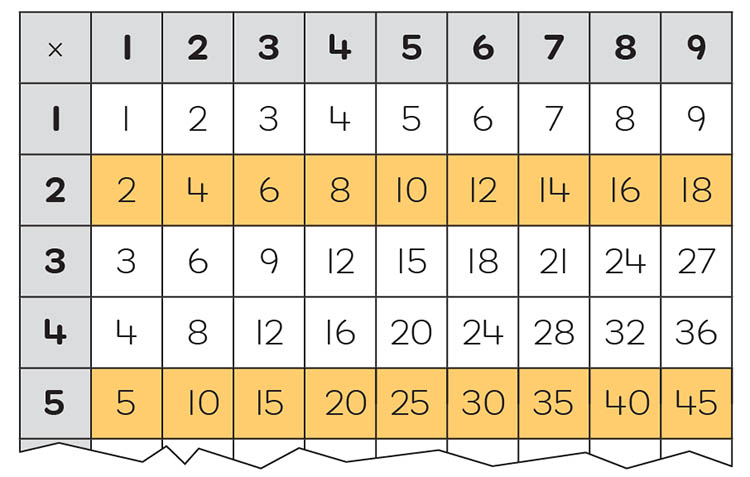
The above techniques can be used to find equivalent fractions for a single fraction. But how do you solve this problem?

7/12 + 5/9

One method is to multiply both denominators to create an equivalent expression that uses the same denominators (108). But it would be easier to work with these fractions if the  common denominator was as small as possible. This is why the ACM has introduced work with Lowest Common Multiples/Denominators within AC9M5N10 in Year 5 and AC9M6N05 in Year 6. For the above example, the lowest common multiple is 36 and the problem would be solved as follows:

7/12 + 5/9

= 21/36 + 20/36

= 41/36

Students would need then to check that 41/36 is in its simplest form. If they can recognise that 41 is a prime number, they would know that it is already in simplest form. However, if they are dealing with 3-digit numerators and denominators or beyond, it would help if they have a knowledge of divisibility rules. For example, suppose the original problem above (7/12 + 5/9) was solved by simply multiplying the denominators. The solution would be shown as follows:

7/12 + 5/9

= 63/108 + 60/108

= 123/108

To simplify 123/108 the student would benefit from knowing some basic divisibility rules. In this case, if you added the digits of each number within the fraction, the sum of each is a multiple of 3 and therefore is divisible by 3. Other divisibility tests would show that 3 is the only factor, and therefore the highest common factor of 123 and 108. This means 41/36 is the simplest form. Again, this is why the ACM has introduced work in Year 5 with Highest Common Factors (see AC9M5N10) and tests of divisibility (see AC9M5N02).

The underlying message in this article is the increased focus on equivalence – as this understanding drives success with percentage and the operation of fractions. It could be argued that the ‘new’ changes will have significant impact on Year 5 teachers, as they encounter percentage for the first time, and introduce work with lowest common multiplies, highest common factors and rules for divisibility. Year 6 teachers will be required to build on this foundation.

To learn more about the roll out of the Australian Curriculum V9.0 (Mathematics), register and join us in our upcoming webinar series, hosted by James Burnett and Dr Calvin Irons. Live sessions commence 11 May.
https://www.origoeducation.com.au/term2_2023/